Proposition: 3.32: Angles made by Chord with Tangent

(Proposition 32 from Book 3 of Euclid's “Elements”)

If some straight line touches a circle, and some (other) straight line is drawn across, from the point of contact into the circle, cutting the circle (in two), then those angles the (straight line) makes with the tangent will be equal to the angles in the alternate segments of the circle.

For let some straight line $EF$ touch the circle $ABCD$ at the point $B$, and let some (other) straight line $BD$ have been drawn from point $B$ into the circle $ABCD$, cutting it (in two).
I say that the angles $BD$ makes with the tangent $EF$ will be equal to the angles in the alternate segments of the circle.

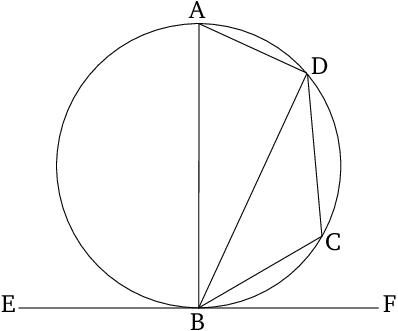
fig32e

Modern Formulation

In a circle, let $\overline{BA}$ be its diameter and $\boxdot{ABCD}$ be a quadrilateral inscribed in the circle and let a tangent $EF$ touch the circle at the point $B$ and let the straight line $BD$ cut the circle (see figure). Then following rectilinear angles are equal: $$\angle{FBD}=\angle{BAD},\quad \angle{DBE}=\angle{DCB}.$$

Proofs: 1

Proofs: 1 2 3

Thank you to the contributors under CC BY-SA 4.0!