◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--4-inscription-and-circumscription / Proof: By Euclid

Proof: By Euclid

(related to Proposition: 4.10: Construction of Isosceles Triangle whose Base Angle is Twice Apex)

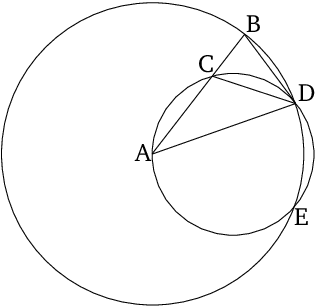
• Let some straight line $AB$ be taken, and let it have been cut at point $C$ so that the rectangle contained by $AB$ and $BC$ is equal to the square on $CA$ [Prop. 2.11].
• And let the circle $BDE$ have been drawn with center $A$, and radius $AB$.
• And let the straight line $BD$, equal to the straight line $AC$, being not greater than the diameter of circle $BDE$, have been inserted into circle $BDE$ [Prop. 4.1].
• And let $AD$ and $DC$ have been joined.

• And let the circle $ACD$ have been circumscribed about triangle $ACD$ [Prop. 4.5].

• And since the (rectangle contained) by $AB$ and $BC$ is equal to the (square) on $AC$, and $AC$ (is) equal to $BD$, the (rectangle contained) by $AB$ and $BC$ is thus equal to the (square) on $BD$.

• And since some point $B$ has been taken outside of circle $ACD$, and two straight lines $BA$ and $BD$ have radiated from $B$ towards the circle $ACD$, and (one) of them cuts (the circle), and (the other) meets (the circle), and the (rectangle contained) by $AB$ and $BC$ is equal to the (square) on $BD$, $BD$ thus touches circle $ACD$ [Prop. 3.37].
• Therefore, since $BD$ touches (the circle) , and $DC$ has been drawn across (the circle) from the point of contact $D$, the angle $BDC$ is thus equal to the angle $DAC$ in the alternate segment of the circle [Prop. 3.32].
• Therefore, since $BDC$ is equal to $DAC$, let $CDA$ have been added to both.
• Thus, the whole of $BDA$ is equal to the two (angles) $CDA$ and $DAC$.
• But, the external (angle) $BCD$ is equal to $CDA$ and $DAC$ [Prop. 1.32].
• Thus, $BDA$ is also equal to $BCD$.
• But, $BDA$ is equal to $CBD$, since the side $AD$ is also equal to $AB$ [Prop. 1.5].
• So that $DBA$ is also equal to $BCD$.
• Thus, the three (angles) $BDA$, $DBA$, and $BCD$ are equal to one another.
• And since angle $DBC$ is equal to $BCD$, side $BD$ is also equal to side $DC$ [Prop. 1.6].
• But, $BD$ was assumed (to be) equal to $CA$.
• Thus, $CA$ is also equal to $CD$.
• So that angle $CDA$ is also equal to angle $DAC$ [Prop. 1.5].
• Thus, $CDA$ and $DAC$ is double $DAC$.
• But $BCD$ (is) equal to $CDA$ and $DAC$.
• Thus, $BCD$ is also double $CAD$.
• And $BCD$ (is) equal to to each of $BDA$ and $DBA$.
• Thus, $BDA$ and $DBA$ are each double $DAB$.
• Thus, the isosceles triangle $ABD$ has been constructed having each of the angles at the base $BD$ double the remaining (angle).
• (Which is) the very thing it was required to do.
  ∎

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"