Proposition: 3.27: Angles on Equal Arcs are Equal

(Proposition 27 from Book 3 of Euclid's “Elements”)

In equal circles, angles standing upon equal circumferences are equal to one another, whether they are standing at the center or at the circumference.

For let the angles $BGC$ and $EHF$ at the centers $G$ and $H$, and the (angles) $BAC$ and $EDF$ at the circumferences, stand upon the equal circumferences $BC$ and $EF$, in the equal circles $ABC$ and $DEF$ (respectively).
I say that angle $BGC$ is equal to (angle) $EHF$, and $BAC$ is equal to $EDF$.

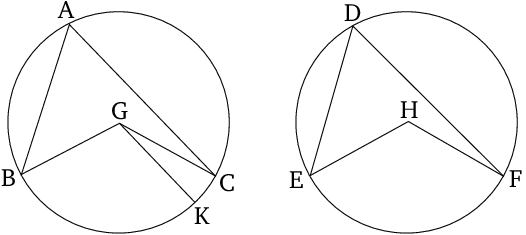
fig27e

Modern Formulation

Let two given circles be congruent and let some of its arcs be also congruent ($BC=EF$). Then the corresponding inscribed angles are also congruent ($\angle{BAC}=\angle{EDF}$) and the corresponding central angles are also congruent ($\angle{BGC}=\angle{EHF}$) are also congruent.

This is the converse of the Prop. 3.26.

Proofs: 1

Proofs: 1 2 3 4 5 6 7
Propositions: 8

Thank you to the contributors under CC BY-SA 4.0!