Equal circles are (circles) whose diameters are equal, or whose (distances) from the centers (to the circumferences) are equal (i.e., whose radii are equal).
Two circles \(\odot AB\) and \(\odot CD\) are called congruent (written \(\odot AB\cong\odot CD\)), if their radii are equal, otherwise they are unequal (written \(\odot AB\neq CD\)).
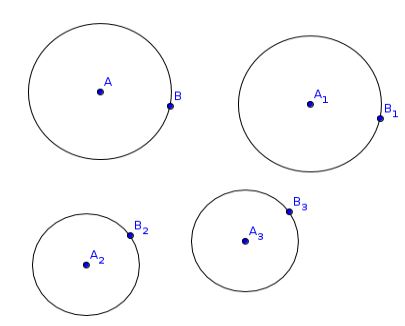
In the following figure, we have the following congruences: \(\odot AB\cong\odot A_1B_1\) and \(\odot A_2B_2\cong\odot A_3B_3\), however, \(\odot AB\ncong\odot A_2B_2\).
Proofs: 1 2 3 4 5 6
Propositions: 7 8 9 10 11