◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--3-circles / Proposition: 3.33: Construction of Segment on Given Line Admitting Given Angle

Proposition: 3.33: Construction of Segment on Given Line Admitting Given Angle

(Proposition 33 from Book 3 of Euclid's “Elements”)

To draw a segment of a circle, accepting an angle equal to a given rectilinear angle, on a given straight line.

• Let $AB$ be the given straight line, and $C$ the given rectilinear angle.
• So it is required to draw a segment of a circle, accepting an angle equal to $C$, on the given straight line $AB$.

Modern Formulation

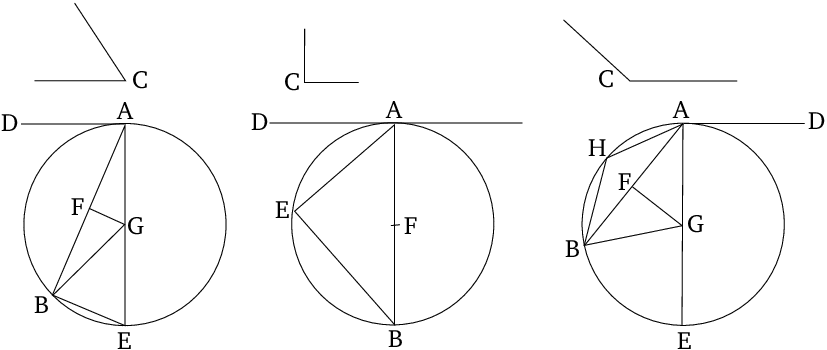
It is possible to construct segment of a circle, such that its inscribed angle (in the three illustrated cases above the respective angles $\angle{ABE}$, $\angle{AEB}$, and $\angle{AHB}$) is equal to a given rectilinear angle (in the three illustrated cases above the respective acute $\angle{C}$ , right $\angle{C}$, and obtuse $\angle{C}$) and its legs are adjacent to a given chord ($\overline{AB}$) of this circle.

Table of Contents

Proofs: 1

Mentioned in:

Sections: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016