Proposition: 3.35: Intersecting Chord Theorem

(Proposition 35 from Book 3 of Euclid's “Elements”)

If two straight lines in a circle cut one another then the rectangle contained by the pieces of one is equal to the rectangle contained by the pieces of the other.

For let the two straight lines $AC$ and $BD$, in the circle $ABCD$, cut one another at point $E$.
I say that the rectangle contained by $AE$ and $EC$ is equal to the rectangle contained by $DE$ and $EB$.

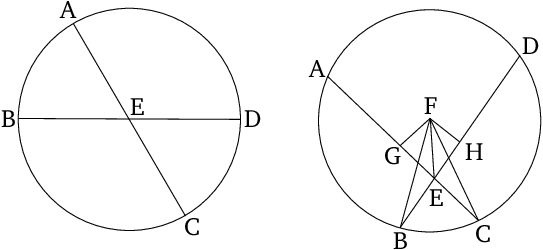
fig35e

Modern Formulation

If in a circle two chords $\overline{AC},$ $\overline{BD}$ intersect at the point $E$ and let the lengths of segments be defined by $|\overline{AE}|$, $|\overline{EC}|$, $|\overline{DE}|$, and $|\overline{EB}|.$ Then the respective rectangles built from these segments have equal areas, i.e. $$|\overline{AE}|\cdot|\overline{EC}|=|\overline{DE}\cdot|\overline{EB}|.$$

Proofs: 1

Sections: 1

Thank you to the contributors under CC BY-SA 4.0!