◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--2-geometric-algebra / Definition: 2.1: Area of Rectangle, Rectangle Contained by Adjacent Sides

Definition: 2.1: Area of Rectangle, Rectangle Contained by Adjacent Sides

Any rectangular parallelogram is said to be contained by the two straight lines containing the right angle.

Modern Formulation

A rectangle is said to be contained by any two adjacent sides. Thus, the rectangle \(\boxdot{ABCD}\) is said to be contained by \(\overline{AB}\), \(\overline{AD}\), or by \(\overline{AB}\), \(\overline{BC}\), etc.

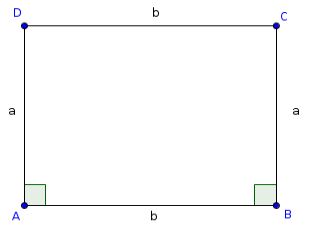
The area of a rectangle contained by two sides is denoted by the product of their lengths. Thus, the area of the rectangle \(\boxdot{ABCD}\) is \(\overline{AB}\cdot \overline{AD}\), or \(\overline{AB}\cdot \overline{BC}\), etc.

Table of Contents

1. Definition: Point of Division, Point of External Division

Mentioned in:

Chapters: 1
Definitions: 2
Lemmas: 3 4 5 6
Proofs: 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
Propositions: 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"