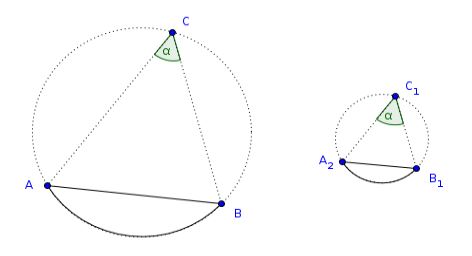
Similar segments of circles are those accepting equal angles, or in which the angles are equal to one another.
If we are given two circles with circular segments \(AB\) and \(A_1B_1\) such that the angles \(\alpha\) in the respective circular segments are equal, then the segments \(AB\) and \(A_1B_1\) are similar.
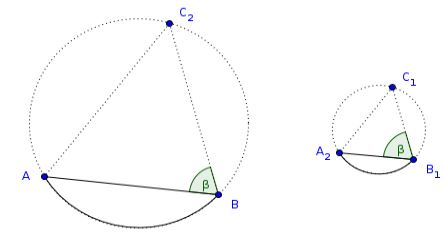
Also, of the angles \(\beta\) contained by the chords \(\overline{AB}\), \(\overline{A_1B_1}\) of the respective segments and the straight line connecting one endpoint of these chords (without loss of generality \(B\), \(B_1\)) and some points of the circumferences of the circles \(C\) and \(C_1\), then the segments \(AB\) and \(A_1B_1\) are similar.