◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--5-proportion / Proposition: 5.06: Multiplication of Real Numbers is Right Distributive over Subtraction

Proposition: 5.06: Multiplication of Real Numbers is Right Distributive over Subtraction

(Proposition 6 from Book 5 of Euclid's “Elements”)

If two magnitudes are equal multiples of two (other) magnitudes, and some (parts) taken away (from the former magnitudes) are equal multiples of the latter (magnitudes, respectively), then the remainders are also either equal to the latter (magnitudes), or (are) equal multiples of them (respectively).

• For let two magnitudes $AB$ and $CD$ be equal multiples of two magnitudes $E$ and $F$ (respectively).
• And let the (parts) taken away (from the former) $AG$ and $CH$ be equal multiples of $E$ and $F$ (respectively).
• I say that the remainders $GB$ and $HD$ are also either equal to $E$ and $F$ (respectively), or (are) equal multiples of them.

Modern Formulation

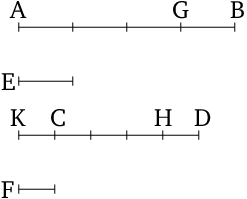
If we are given two positive real numbers \(\alpha\), \(\beta\),¹ and the following multiples of aliquot parts \(m\ge 1\), \(n\ge 1\): \[m\alpha=m\beta,\quad n\alpha=n\beta\quad\quad( * )\] then adding both equations gives us \[(m-n)\alpha=m\beta-n\beta.\]

General Modern Formulation

See distributivity law for real numbers.

Table of Contents

Proofs: 1

Mentioned in:

Sections: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016

Footnotes