Proposition: 6.15: Characterization of Congruent Triangles

(Proposition 15 from Book 6 of Euclid's “Elements”)

In equal triangles also having one angle equal to one (angle) the sides about the equal angles are reciprocally proportional. And those triangles having one angle equal to one angle for which the sides about the equal angles (are) reciprocally proportional are equal.

Let $ABC$ and $ADE$ be equal triangles having one angle equal to one (angle), (namely) $BAC$ (equal) to $DAE$.
I say that, in triangles $ABC$ and $ADE$, the sides about the equal angles are reciprocally proportional, that is to say, that as $CA$ is to $AD$, so $EA$ (is) to $AB$.

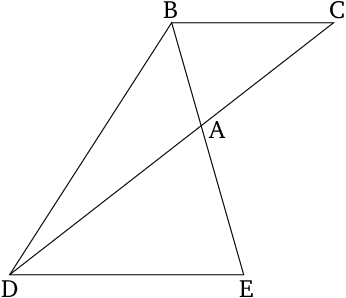
fig15e

Modern Formulation

Two triangles are congruent if and only if they have one angle equal and the products¹ of the side lengths of this angle are in both triangles equal.

$$\begin{array}{rclc} \bigtriangleup{ABC}\cong\bigtriangleup{ADE}&\Longleftrightarrow&(\angle{BAC}=\angle{DAE})&\wedge\\ &&(|\overline{CA}|\cdot|\overline{AB}|=|\overline{EA}|\cdot|\overline{AD}|). \end{array}$$

Proofs: 1

Proofs: 1 2

Thank you to the contributors under CC BY-SA 4.0!

Github:
non-Github:: @Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016

Footnotes

The product is equivalent to Euclid's "reciprocal proportion" $$\frac{|\overline{CA}|}{|\overline{AD}|}=\frac{|\overline{EA}|}{|\overline{AB}|},$$ which is not to be confused with the concept of reciprocal ratio. ↩

◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--6-similar-figures / Proposition: 6.15: Characterization of Congruent Triangles