Branches History Index

◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--6-similar-figures / Proposition: 6.29: Construction of Parallelogram Equal to Given Figure Exceeding a Parallelogram

Proposition: 6.29: Construction of Parallelogram Equal to Given Figure Exceeding a Parallelogram

(Proposition 9 from Book 6 of Euclid's “Elements”)

To apply a parallelogram, equal to a given rectilinear figure, to a given straight line, (the applied parallelogram) overshooting by a parallelogrammic figure similar to a given (parallelogram).

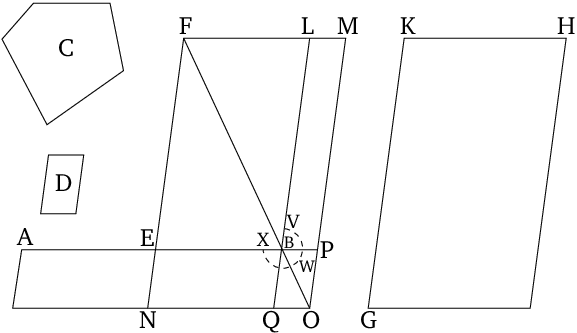
fig29e

Modern Formulation

This proposition is a geometric solution of the quadratic equation1 \[x^2 + \alpha\,x -\beta = 0.\]

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:
bookofproofs
non-Github:
@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

  1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

  1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016

Footnotes

  1. Here, $x$ is the ratio of a side of the excess to the corresponding side of figure $D$, $\alpha$ is the ratio of the length of $AB$ to the length of that side of figure $D$ which corresponds to the side of the excess running along $AB$, and $\beta$ is the ratio of the areas of figures $C$ and $D$. Only the positive root of the equation is found (translator's note). ↩