◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Definition: 1.19: Rectilinear Figure, Sides, n-Sided Figure

Definition: 1.19: Rectilinear Figure, Sides, n-Sided Figure

Rectilinear figures are those (figures) contained by straight lines: trilateral figures being those contained by three straight lines, quadrilateral by four, and multilateral by more than four.

Modern Definition

A n-sided figure (or a rectilinear figure) is a figure given by a finite number \(n\ge 3\) of segments \(\overline{A_1B_1},\overline{A_2B_2},\ldots,\overline{A_nB_n}\), also called its sides, in such a way that

1. \(A_1=B_2, A_2=B_3, \ldots, A_{n-1}=B_n,A_{n}=B_1\), and that
2. all sides do not have any other points in common except their endpoints, and
3. each endpoint is the endpoint of exactly two sides.

We denote n-sided figures beginning with an arbitrary point and listing all points counter-clockwise.

Example

An 11-sided figure \( B A K J I H G F E D C \):

|

Table of Contents

1. Definition: Triangle
2. Definition: Pentagon
3. Definition: Hexagon
4. Definition: Decagon

Mentioned in:

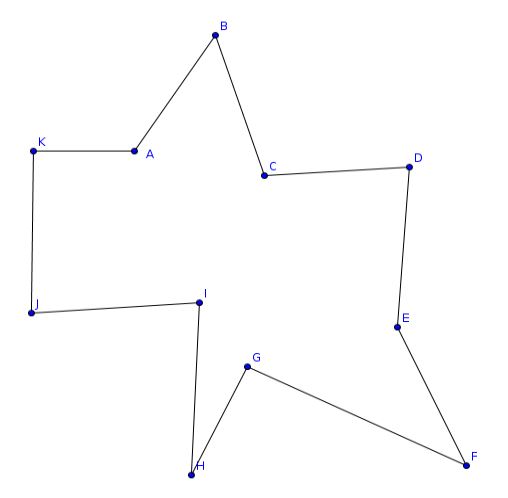Chapters: 1
Corollaries: 2 3 4 5
Definitions: 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Proofs: 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55
Propositions: 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"