To apply a parallelogram, equal to a given rectilinear figure, to a given straight line, (the applied parallelogram) falling short by a parallelogrammic figure similar to a given (parallelogram). It is necessary for the given rectilinear figure [to which it is required to apply an equal (parallelogram)] not to be greater than the (parallelogram) described on half (of the straight line) and similar to the deficit.
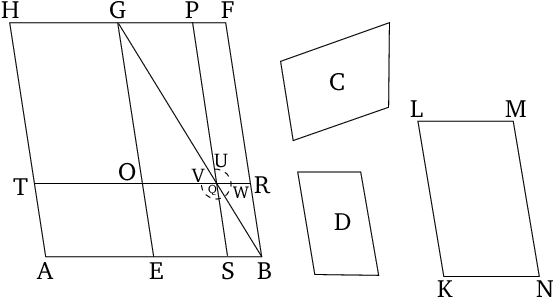
This proposition is a geometric solution of the quadratic equation1 \[x^2 - \alpha\,x +\beta = 0.\]
Proofs: 1
Here, $x$ is the ratio of a side of the deficit to the corresponding side of figure $D$, $\alpha$ is the ratio of the length of $AB$ to the length of that side of figure $D$ which corresponds to the side of the deficit running along $AB$, and $\beta$ is the ratio of the areas of figures $C$ and $D$. The constraint corresponds to the condition $\beta < \alpha^2/4$ for the equation to have real roots. Only the smaller root of the equation is found. The larger root can be found by a similar method (translator's note). ↩