Corollary: 6.08: Geometric Mean Theorem

(Corollary to Proposition 8 from Book 6 of Euclid's “Elements”)

So (it is) clear, from this, that if, in a right-angled triangle, a (straight line) is drawn from the right angle perpendicular to the base then the (straight line so) drawn is in mean proportion to the pieces of the base. (Which is) the very thing it was required to show.

Modern Formulation (Geometric Mean Theorem)

In any right-angled triangle with the sides \(a\), \(b\) with a right angle between the sides \(a\) and \(b\), the (segment) \(h\) drawn from the right angle perpendicular to the base \(c\) will cut it into pieces \(p\) and \(q\) and is equal the geometric mean of these pieces, formally

\[h=\sqrt{pq}.\]

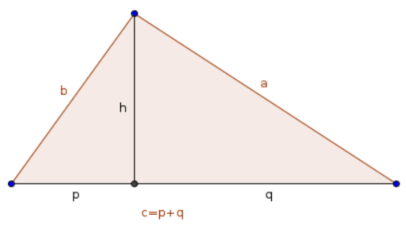
meanproportion