◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--6-similar-figures / Proposition: 6.20: Similar Polygons are Composed of Similar Triangles

Proposition: 6.20: Similar Polygons are Composed of Similar Triangles

(Proposition 20 from Book 6 of Euclid's “Elements”)

Similar polygons can be divided into equal numbers of similar triangles corresponding (in proportion) to the wholes, and one polygon has to the (other) polygon a squared ratio with respect to (that) a corresponding side (has) to a corresponding side.

• Let $ABCDE$ and $FGHKL$ be similar polygons, and let $AB$ correspond to $FG$.
• I say that polygons $ABCDE$ and $FGHKL$ can be divided into equal numbers of similar triangles corresponding (in proportion) to the wholes, and (that) polygon $ABCDE$ has a squared ratio to polygon $FGHKL$ with respect to that $AB$ (has) to $FG$.

Modern Formulation

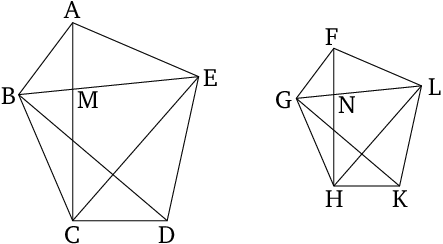
The ratio of the areas of two similar rectilinear figures is proportional to the squared ratio of the lengths of corresponding sides.¹

Table of Contents

Proofs: 1 Corollaries: 1

Mentioned in:

Corollaries: 1
Proofs: 2 3 4

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016

Footnotes