Definition: 7.16: Rectangular Number, Plane Number

And when two numbers multiplying one another make some (other number) then the (number so) created is called plane, and its sides (are) the numbers which multiply one another.

Modern Formulation

A rectangular number \(h\) is the product of two positive integers \(a\) and \(b\):

\[h=a\cdot b.\]

Notes

Instead of Euclid's term "plane number", the term "rectangular number" is used more often.
The rectangular number can be interpreted as the area of a rectangle with the sides of integer lengths \(a\) and \(b\), e.g. in the following figure, \(a=2\), \(b=4\) and \(h=8\).

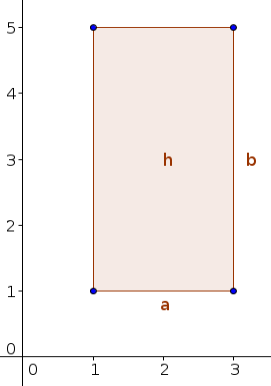
productnumber

This formula, of course, holds not only for rectangles, whose sides have integer lengths but also for sides with lengths represented by positive real numbers. However, in the 7th Book of "The Elements", Euclid deals with positive integers only.

Definitions: 1 2 3

Thank you to the contributors under CC BY-SA 4.0!