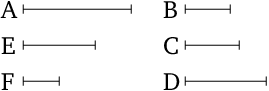Proof: By Euclid
(related to Theorem: Prop. 9.14: Fundamental Theorem of Arithmetic)
- For let $A$ be the least number measured by the prime numbers $B$, $C$, $D$.
- I say that $A$ will not be measured by any other prime number except (one of) $B$, $C$, $D$.
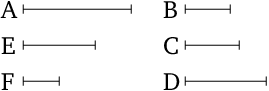
- For, if possible, let it be measured by the prime (number) $E$.
- And let $E$ not be the same as one of $B$, $C$, $D$.
- And since $E$ measures $A$, let it measure it according to $F$.
- Thus, $E$ has made $A$ (by) multiplying $F$.
- And $A$ is measured by the prime numbers $B$, $C$, $D$.
- And if two numbers make some (number by) multiplying one another, and some prime number measures the number created from them, then (the prime number) will also measure one of the original (numbers) [Prop. 7.30].
- Thus, $B$, $C$, $D$ will measure one of $E$, $F$.
- In fact, they do not measure $E$.
- For $E$ is prime, and not the same as one of $B$, $C$, $D$.
- Thus, they (all) measure $F$, which is less than $A$.
- The very thing (is) impossible.
- For $A$ was assumed (to be) the least (number) measured by $B$, $C$, $D$.
- Thus, no prime number can measure $A$ except (one of) $B$, $C$, $D$.
- (Which is) the very thing it was required to show.
∎
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

- non-Github:
- @Fitzpatrick
References
Adapted from (subject to copyright, with kind permission)
- Fitzpatrick, Richard: Euclid's "Elements of Geometry"