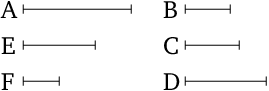◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--9-number-theory-applications / Theorem: Prop. 9.14: Fundamental Theorem of Arithmetic

Theorem: Prop. 9.14: Fundamental Theorem of Arithmetic

(Proposition 14 from Book 9 of Euclid's “Elements”)

If a least number is measured by (some) prime numbers then it will not be measured by any other prime number except (one of) the original measuring (numbers).

• For let $A$ be the least number measured by the prime numbers $B$, $C$, $D$.
• I say that $A$ will not be measured by any other prime number except (one of) $B$, $C$, $D$.

Modern Formulation

see fundamental theorem of arithmetic.

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Bibliography

1. Kramer Jürg, von Pippich, Anna-Maria: "Von den natürlichen Zahlen zu den Quaternionen", Springer-Spektrum, 2013

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"