Proposition: 9.35: Sum of Geometric Progression
(Proposition 35 from Book 9 of Euclid's “Elements”)
If there is any multitude whatsoever of numbers in continued proportion, and (numbers) equal to the first are subtracted from (both) the second and the last, then as the excess of the second (number is) to the first, so the excess of the last will be to (the sum of) all those (numbers) before it.
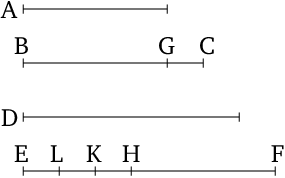
- Let $A$, $BC$, $D$, $EF$ be any multitude whatsoever of numbers in continued proportion, beginning from the least $A$.
- And let $BG$ and $FH$, each equal to $A$, have been subtracted from $BC$ and $EF$ (respectively).
- I say that as $GC$ is to $A$, so $EH$ is to $A$, $BC$, $D$.
Modern Formulation
see sum of geometric progression.
Table of Contents
Proofs: 1
Mentioned in:
Proofs: 1 2 3
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

