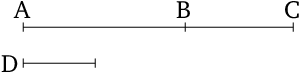◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-10-incommensurable-magnitudes / Proof: By Euclid

Proof: By Euclid

(related to Proposition: Prop. 10.015: Commensurability of Sum of Commensurable Magnitudes)

• For let the two commensurable magnitudes $AB$ and $BC$ be laid down together.
• I say that the whole $AC$ is also commensurable with each of $AB$ and $BC$.

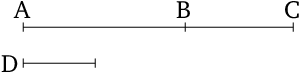
• For since $AB$ and $BC$ are commensurable, some magnitude will measure them.
• Let it (so) measure (them), and let it be $D$.
• Therefore, since $D$ measures (both) $AB$ and $BC$, it will also measure the whole $AC$.
• And it also measures $AB$ and $BC$.
• Thus, $D$ measures $AB$, $BC$, and $AC$.
• Thus, $AC$ is commensurable with each of $AB$ and $BC$ [Def. 10.1] .
• And so let $AC$ be commensurable with $AB$.
• I say that $AB$ and $BC$ are also commensurable.
• For since $AC$ and $AB$ are commensurable, some magnitude will measure them.
• Let it (so) measure (them), and let it be $D$.
• Therefore, since $D$ measures (both) $CA$ and $AB$, it will thus also measure the remainder $BC$.
• And it also measures $AB$.
• Thus, $D$ will measure (both) $AB$ and $BC$.
• Thus, $AB$ and $BC$ are commensurable [Def. 10.1] .
• Thus, if two magnitudes, and so on ....
  ∎

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"