Proposition: Prop. 10.050: Construction of Third Binomial Straight Line

Euclid's Formulation

To find a third binomial (straight line).

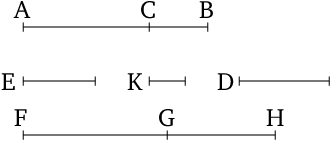
Let the two numbers $AC$ and $CB$ be laid down such that their sum $AB$ has to $BC$ the ratio which (some) square number (has) to (some) square number, and does not have to $AC$ the ratio which (some) square number (has) to (some) square number.
And let some other non-square number $D$ also be laid down, and let it not have to each of $BA$ and $AC$ the ratio which (some) square number (has) to (some) square number.
And let some rational straight line $E$ be laid down, and let it have been contrived that as $D$ (is) to $AB$, so the (square) on $E$ (is) to the (square) on $FG$ [Prop. 10.6 corr.] .
Thus, the (square) on $E$ is commensurable with the (square) on on $FG$ [Prop. 10.6].
And $E$ is a rational (straight line).
Thus, $FG$ is also a rational (straight line).
And since $D$ does not have to $AB$ the ratio which (some) square number has to (some) square number, the (square) on $E$ does not have to the (square) on $FG$ the ratio which (some) square number (has) to (some) square number either.
$E$ is thus incommensurable in length with $FG$ [Prop. 10.9].
So, again, let it have been contrived that as the number $BA$ (is) to $AC$, so the (square) on $FG$ (is) to the (square) on $GH$ [Prop. 10.6 corr.] .
Thus, the (square) on $FG$ is commensurable with the (square) on on $GH$ [Prop. 10.6].
And $FG$ (is) a rational (straight line).
Thus, $GH$ (is) also a rational (straight line).
And since $BA$ does not have to $AC$ the ratio which (some) square number (has) to (some) square number, the (square) on $FG$ does not have to the (square) on $HG$ the ratio which (some) square number (has) to (some) square number either.
Thus, $FG$ is incommensurable in length with $GH$ [Prop. 10.9].
$FG$ and $GH$ are thus rational (straight lines which are) commensurable in square only.
Thus, $FH$ is a binomial (straight line) [Prop. 10.36].
So, I say that (it is) also a third (binomial straight line).

fig050e

Modern Formulation

If the rational straight line has unit length then the length of a third binomial straight line is \[\sqrt{\alpha}\,\left(1+\sqrt{1-\beta^{\,2}}\right),\]

where $\alpha,\beta$ denote positive rational numbers.

Notes

This, and the third apotome, whose length according to [Prop. 10.87] is \[\sqrt{\alpha}\,\left(1-\sqrt{1-\beta^{\,2}}\right),\] are the roots of the quadratic function \[x^2- 2\,\sqrt{\alpha}\,x+\alpha\,\beta^{\,2}=0,\]

where $\alpha,\beta$ denote positive rational numbers.

Proofs: 1

Propositions: 1

Thank you to the contributors under CC BY-SA 4.0!