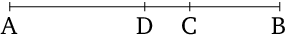◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-10-incommensurable-magnitudes / Lemma: Lem. 10.059: Sum of Squares on Unequal Pieces of Segment Is Greater than Twice the Rectangle Contained by Them

Lemma: Lem. 10.059: Sum of Squares on Unequal Pieces of Segment Is Greater than Twice the Rectangle Contained by Them

(Lemma to Proposition 59 from Book 10 of Euclid's “Elements”)

If a straight line is cut unequally then (the sum of) the squares on the unequal (parts) is greater than twice the rectangle contained by the unequal (parts).

• Let $AB$ be a straight line, and let it have been cut unequally at $C$, and let $AC$ be greater (than $CB$).
• I say that (the sum of) the (squares) on $AC$ and $CB$ is greater than twice the (rectangle contained) by $AC$ and $CB$.

Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"