◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proposition: Prop. 12.15: Cones or Cylinders are Equal iff Bases are Reciprocally Proportional to Heights

Proposition: Prop. 12.15: Cones or Cylinders are Equal iff Bases are Reciprocally Proportional to Heights

Euclid's Formulation

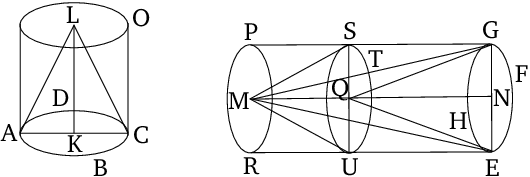
The bases of equal cones and cylinders are reciprocally proportional to their heights. And, those cones and cylinders whose bases (are) reciprocally proportional to their heights are equal.

• Let there be equal cones and cylinders whose bases are the circles $ABCD$ and $EFGH$, and the diameters of (the bases) $AC$ and $EG$, and (whose) axes (are) $KL$ and $MN$, which are also the heights of the cones and cylinders (respectively).
• And let the cylinders $AO$ and $EP$ have been completed.
• I say that the bases of cylinders $AO$ and $EP$ are reciprocally proportional to their heights, and (so) as base $ABCD$ is to base $EFGH$, so height $MN$ (is) to height $KL$.

Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016