◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proof: By Euclid

Proof: By Euclid

(related to Proposition: Prop. 12.15: Cones or Cylinders are Equal iff Bases are Reciprocally Proportional to Heights)

• Let there be equal cones and cylinders whose bases are the circles $ABCD$ and $EFGH$, and the diameters of (the bases) $AC$ and $EG$, and (whose) axes (are) $KL$ and $MN$, which are also the heights of the cones and cylinders (respectively).
• And let the cylinders $AO$ and $EP$ have been completed.
• I say that the bases of cylinders $AO$ and $EP$ are reciprocally proportional to their heights, and (so) as base $ABCD$ is to base $EFGH$, so height $MN$ (is) to height $KL$.

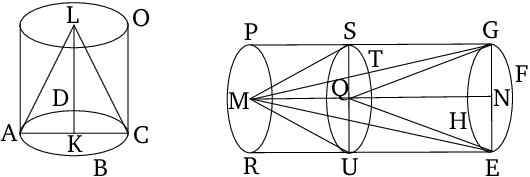
• For height $LK$ is either equal to height $MN$, or not.
• Let it, first of all, be equal.
• And cylinder $AO$ is also equal to cylinder $EP$.
• And cones and cylinders having the same height are to one another as their bases [Prop. 12.11].
• Thus, base $ABCD$ (is) also equal to base $EFGH$.
• And, hence, reciprocally, as base $ABCD$ (is) to base $EFGH$, so height $MN$ (is) to height $KL$.
• And so, let height $LK$ not be equal to $MN$, but let $MN$ be greater.
• And let $QN$, equal to $KL$, have been cut off from height $MN$.
• And let the cylinder $EP$ have been cut, through point $Q$, by the plane $TUS$ (which is) parallel to the planes of the circles $EFGH$ and $RP$.
• And let cylinder $ES$ have been conceived, with base the circle $EFGH$, and height $NQ$.
• And since cylinder $AO$ is equal to cylinder $EP$, thus, as cylinder $AO$ (is) to cylinder $ES$, so cylinder $EP$ (is) to cylinder $ES$ [Prop. 5.7].
• But, as cylinder $AO$ (is) to cylinder $ES$, so base $ABCD$ (is) to base $EFGH$.
• For cylinders $AO$ and $ES$ (have) the same height [Prop. 12.11].
• And as cylinder $EP$ (is) to (cylinder) $ES$, so height $MN$ (is) to height $QN$.
• For cylinder $EP$ has been cut by a plane which is parallel to its opposite planes [Prop. 12.13].
• And, thus, as base $ABCD$ is to base $EFGH$, so height $MN$ (is) to height $QN$ [Prop. 5.11].
• And height $QN$ (is) equal to height $KL$.
• Thus, as base $ABCD$ is to base $EFGH$, so height $MN$ (is) to height $KL$.
• Thus, the bases of cylinders $AO$ and $EP$ are reciprocally proportional to their heights. And, so, let the bases of cylinders $AO$ and $EP$ be reciprocally proportional to their heights, and (thus) let base $ABCD$ be to base $EFGH$, as height $MN$ (is) to height $KL$.
• I say that cylinder $AO$ is equal to cylinder $EP$.
• For, with the same construction, since as base $ABCD$ is to base $EFGH$, so height $MN$ (is) to height $KL$, and height $KL$ (is) equal to height $QN$, thus, as base $ABCD$ (is) to base $EFGH$, so height $MN$ will be to height $QN$.
• But, as base $ABCD$ (is) to base $EFGH$, so cylinder $AO$ (is) to cylinder $ES$.
• For they are the same height [Prop. 12.11].
• And as height $MN$ (is) to [height] $QN$, so cylinder $EP$ (is) to cylinder $ES$ [Prop. 12.13].
• Thus, as cylinder $AO$ is to cylinder $ES$, so cylinder $EP$ (is) to (cylinder) $ES$ [Prop. 5.11].
• Thus, cylinder $AO$ (is) equal to cylinder $EP$ [Prop. 5.9].
• In the same manner, (the proposition can) also (be demonstrated) for the cones.
• (Which is) the very thing it was required to show.
  ∎

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"