◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proof: By Euclid

Proof: By Euclid

(related to Proposition: Prop. 12.07: Prism on Triangular Base divided into Three Equal Tetrahedra)

• Let there be a prism whose base (is) triangle $ABC$, and opposite (plane) $DEF$.
• I say that prism $ABCDEF$ is divided into three pyramids having triangular bases (which are) equal to one another.

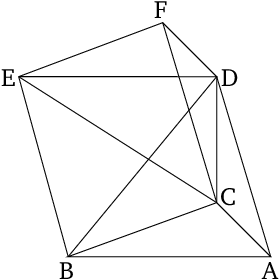
• For let $BD$, $EC$, and $CD$ have been joined.
• Since $ABED$ is a parallelogram, and $BD$ is its diagonal, triangle $ABD$ is thus equal to triangle $EBD$ [Prop. 1.34].
• And, thus, the pyramid whose base (is) triangle $ABD$, and apex the point $C$, is equal to the pyramid whose base is triangle $DEB$, and apex the point $C$ [Prop. 12.5].
• But, the pyramid whose base is triangle $DEB$, and apex the point $C$, is the same as the pyramid whose base is triangle $EBC$, and apex the point $D$.
• For they are contained by the same planes.
• And, thus, the pyramid whose base is $ABD$, and apex the point $C$, is equal to the pyramid whose base is $EBC$ and apex the point $D$.
• Again, since $FCBE$ is a parallelogram, and $CE$ is its diagonal, triangle $CEF$ is equal to triangle $CBE$ [Prop. 1.34].
• And, thus, the pyramid whose base is triangle $BCE$, and apex the point $D$, is equal to the pyramid whose base is triangle $ECF$, and apex the point $D$ [Prop. 12.5].
• And the pyramid whose base is triangle $BCE$, and apex the point $D$, was shown (to be) equal to the pyramid whose base is triangle $ABD$, and apex the point $C$.
• Thus, the pyramid whose base is triangle $CEF$, and apex the point $D$, is also equal to the pyramid whose base [is] [triangle]bookofproofs$6432 $ABD$, and apex the point $C$.
• Thus, the prism $ABCDEF$ has been divided into three pyramids having triangular bases (which are) equal to one another.
• And since the pyramid whose base is triangle $ABD$, and apex the point $C$, is the same as the pyramid whose base is triangle $CAB$, and apex the point $D$.
• For they are contained by the same planes.
• And the pyramid whose base (is) triangle $ABD$, and apex the point $C$, was shown (to be) a third of the prism whose base is triangle $ABC$, and opposite (plane) $DEF$, thus the pyramid whose base is triangle $ABC$, and apex the point $D$, is also a third of the pyramid having the same base, triangle $ABC$, and opposite (plane) $DEF$.
  ∎

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"