◀ ▲ ▶Branches / Geometry / Elements-euclid / Book-12-proportional-stereometry / Proposition: Prop. 12.07: Prism on Triangular Base divided into Three Equal Tetrahedra

Proposition: Prop. 12.07: Prism on Triangular Base divided into Three Equal Tetrahedra

Euclid's Formulation

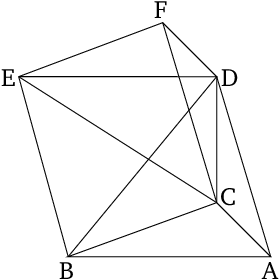
Any prism having a triangular base is divided into three pyramids having triangular bases (which are) equal to one another.

• Let there be a prism whose base (is) triangle $ABC$, and opposite (plane) $DEF$.
• I say that prism $ABCDEF$ is divided into three pyramids having triangular bases (which are) equal to one another.

Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1 Corollaries: 1

Mentioned in:

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016