Let \(G(V,E)\) be a bipartite graph with the corresponding partition of vertices \(V=A\cup B\), \(A\cap B=\emptyset\) and \(|A|=n\) \(|B|=m\), \(n\ge 1\), \(m\ge 1\).
\(G\) is called a complete bipartite graph and denoted by \(K_{m,n}\), if each vertex in \(A\) is joined to each vertex in \(B\) by just one edge.
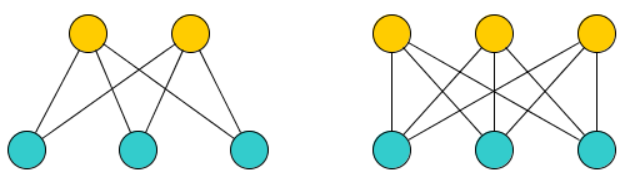
The following figure shows two complete bipartite graphs: \(K_{2,3}\) and \(K_{3,3}\):
Problems: 1
Solutions: 2
Theorems: 3