Definition: Bipartite Graph
A digraph \(D(V,E,\alpha,\omega)\) or an undirected graph \(G(V,E,\gamma)\) is called bipartite, if its vertices can be split into two subsets \(A\) and \(B\) in such a way that each edge of the graph joins a vertex in \(A\) and a vertex in \(B\). Formally, if there is a partition of vertices \(V=A\cup B,~ A\cap B=\emptyset\) with
- Either \(\alpha(e)\in A \wedge \omega(e)\in B)\) or \(\alpha(e)\in B \wedge \omega(e)\in A\) for all \(e\in E\) in a digraph \(D(V,E,\alpha,\omega)\).
- \(\gamma(e)=X\) with some pairs of vertices \(X=\{x,y\}\) such that either \(x\in A, y\in B\) or \(x\in B, y\in A\) for all \(e\in E\) in a graph \(G(V,E,\gamma)\).
In particular, a bipartite graph has no loops.
Example
The following figure shows a bipartite digraph. The vertices of one partition \(A\) are colored blue, while the vertices of the other partition \(B\) are colored orange. Please note that there are only edges between vertices with alternating colors. In particular, there are no loops:
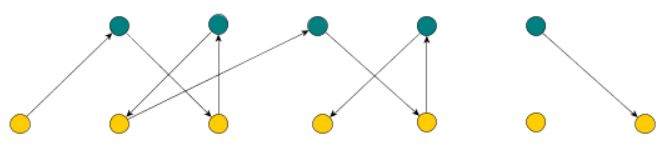
Table of Contents
- Definition: Complete Bipartite Graph
Mentioned in:
Definitions: 1
Proofs: 2
Theorems: 3 4
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

References
Bibliography
- Aldous Joan M., Wilson Robin J.: "Graphs and Applications - An Introductory Approach", Springer, 2000
- Krumke S. O., Noltemeier H.: "Graphentheoretische Konzepte und Algorithmen", Teubner, 2005, 1st Edition
