There are two different types of diagrammatic moves, i.e. moves of a knot diagram, which do not change the knotting information of the underlying curve:
Named after the German mathematician Kurt Reidemeister (1893 - 1971), the following Reidemeister moves are moves of any knot diagram, which interact with the crossings of the underlying curve, but still do not change the information of how the curve is knotted. This lack of changing the knotting information is denoted by the equivalence sign "\(\sim\)".
Reidemeister defined the following three moves for classical crossings:
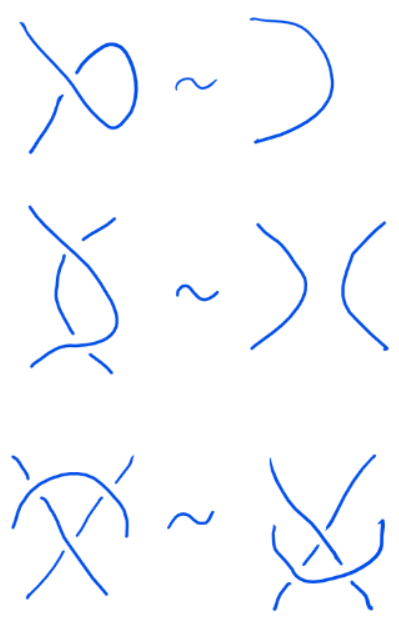
According to Kauffmann[^6914], these moves can be extended to virtual crossings as follows:
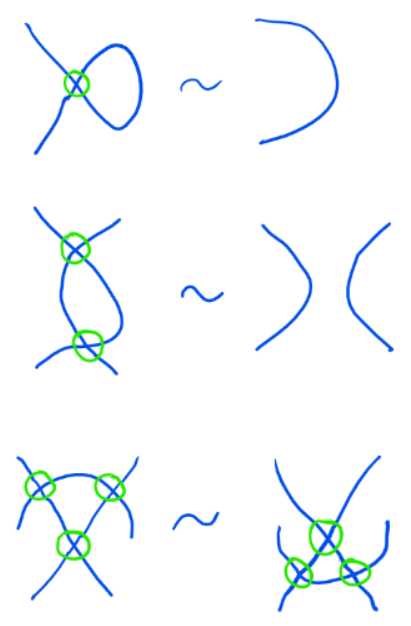
There is a Reidemeister move for mixed (virtual/classical) crossings:

Unlike Reidemeister moves, the planar isotopy moves are local moves of the underlying knot diagram, which do not interact with any crossings. The following example shows two local planar isotopy moves of a diagram:
