(related to Axiom: Peano Axioms)
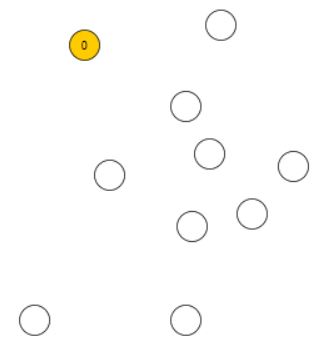
In this article, we try to explain why the Peano axioms define natural numbers. Please consider the following (infinite) set of arbitrary points. As it is not possible to visualize an infinite set in this example, imagine that you see only "a finite subset of this infinite set". This will be good enough for our example:

The first axiom P1 postulates the existence of the element \(0\):
The second axiom P2 postulates that for each element \(n\in N\) there exists a unique element \(n^+\), the so-called successor of n. In order to apply this axiom to our set of points, we need to be careful about two things:
Below, you will find just one of many examples satisfying this condition:
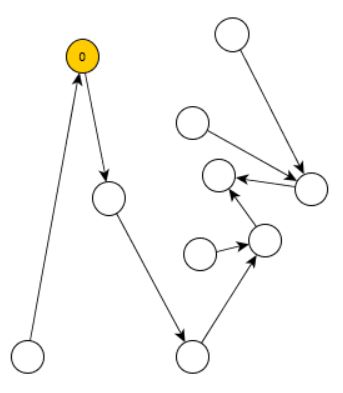
The next axiom P3 states that there is no element \(n\in N\) such that \(n^+=0\) (i.e. \(0\) is not a successor of any element of \(N\)). This eliminates all such points. In our example, there is only one point of this kind, which has to be eliminated:
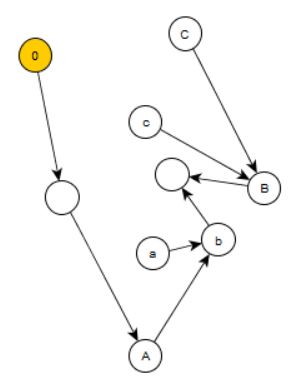
The axiom P4 postulates that if two elements \(n,~m\in N\) have the same successors \(n^+=m^+\) then they are the same \(n=m\). The points \(a,A\), \(b,B\) and \(c,C\) from the previous figure have to be "molten" with each other, resulting in the points \(a\), \(b\), and \(c\) in the following figure:
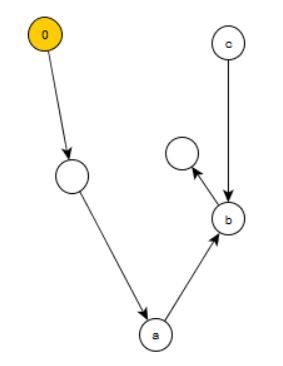
Finally, the axiom P5 (also called the "principle of induction") states that if a subset \(A\subset N\) contains the element \(0\) and with each element \(n\) contained in it it also contains the successor \(n^+\), then \(A\) must be identical with the set of points we are looking for. This eliminates the point \(c\) since it is a subset which does not contain the element \(0\):
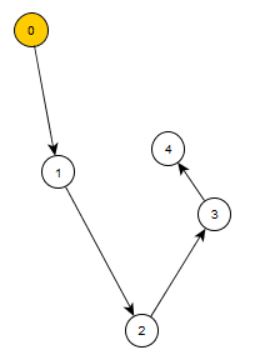
Please note that in the last figure, we have labeled all points by the numbers \(0,1,2,3,\ldots\), although we have started with an abstract set of points. This is just labeling. It does not matter, which infinite labeling system we use (e.g. we could use cuneiform Babylonian numbers etc.). The key feature of the Peano axioms is not the labeling, but the fact that applying them to an arbitrary abstract infinite set of points, as we did in this example, we will always come up with something we can label like this.