◀ ▲ ▶Branches / Number-systems-arithmetics / Explanation: Why is it impossible to divide by `\(0\)`?

Explanation: Why is it impossible to divide by \(0\)?

(related to Proposition: Definition of Real Numbers)

A simple fact taught in the elementary school is that "you cannot divide by 0". However, it is usually not broadly known, why. Here some reasons will be given:

Reason 1

The algebraic reason is that the number \(0\) has no multiplicative inverse. For if it had one, there would exist a number \(0^{-1}\in\mathbb R\), such that \(0\cdot 0^{-1}=1\), following the axiom of the existence of reciprocal numbers. In this case, however, this would contradict another axiom, the distributivity law, more precisely its corollary stating that \(0\cdot x=0\) for all \(x\in\mathbb R\), and in particular for \(x=0^{-1}\) (if it existed)! To avoid this contradiction, the number \(0\) is pragmatically excluded from the multiplicative abelian group \((\mathbb R\setminus \{0\},\cdot)\). In fact, the number \(0\) is not an element of any multiplicative abelian group, in particular (as a special case), not an element of \((\mathbb R\setminus \{0\},\cdot)\).

The pragmatism of this argument (i.e. the avoidance of contradictions) might be not satisfactory enough. So let us consider a more analytical approach:

Reason 2

Imagine that you want to divide a circle (e.g. your pizza) into sectors with an angle \(\alpha=\frac \Pi 2, \frac \Pi 8, \frac \Pi {32}, \frac \Pi {128}, ...\), resulting in the following sectors:

\(\alpha=\Pi/2\approx 1.5708796...\)

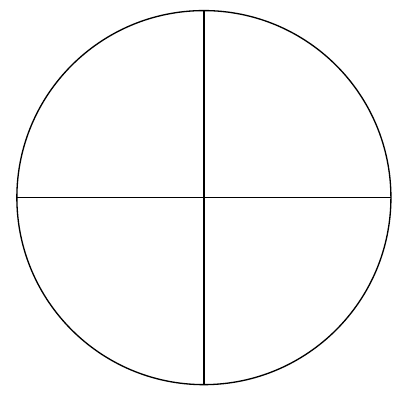
\(\alpha=\Pi/8\approx 0.3926990...\)

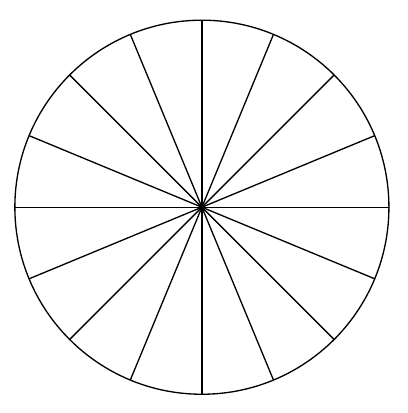
\(\alpha=\Pi/32\approx 0.0981748...\)

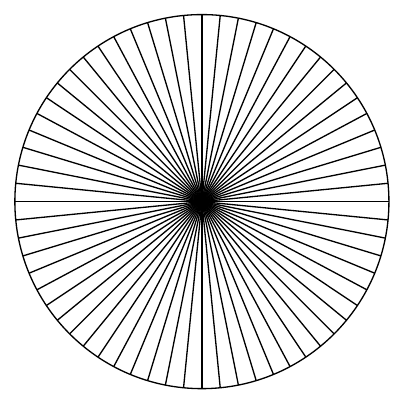
\(\alpha=\Pi/128\approx 0.0245437...\)

As \(\alpha\) gets smaller (i.e. closer to \(0\)), there are more and more pieces you will get. For a very small \(\alpha\), say \(\alpha=\Pi/100000000000000000\), the pieces will get so thin that you won't probably be able to see them (if this is your pizza), and the number of them will get astronomically high. Finally, as \(\alpha\) "almost reaches" \(0\), the number of pieces will "almost reach" infinity. You will probably complain, why do we say "almost reach", but not just "reach"? At least, we wanted to try out, what happens, if we throw away all bans we learned in the school, and divide our pizza by \(0\), after all?

Well, if \(\alpha\) "reaches" zero, we will divide the pizza by \(0\) and get an infinite (\(\infty\)) number of pieces. However, this is impossible in the set \(\mathbb R\), because \(\infty \) is not a real number. At this stage, we have to point out two important things:

1. What we have said above +does not+ mean that we deny the existence of infinity \(\infty \). What we say is that \(\infty\not\in\mathbb R \)! In other words, the division by \(0\) is not possible inside the set of real numbers (since it results in something which is not an element of this set). Actually, whenever a mathematical operation on a set results in an element not of the original set, this indicates that we have broken the chains of one mathematical concept and beginning to create a new, broader concept. This is what science is about!
2. What we have said above +does not+ mean that we deny the existence of infinity \(\infty \). What we say is that \(\infty\not\in\mathbb R \)! In other words, the division by \(0\) is not possible inside the set of real numbers (since it results in something which is not an element of this set). Actually, whenever a mathematical operation on a set results in an element not of the original set, this indicates that we have broken the chains of one mathematical concept and beginning to create a new, broader concept. This is what science is about!

Mentioned in:

Explanations: 1

Thank you to the contributors under CC BY-SA 4.0!

Github: