(related to Definition: Random Experiments and Random Events)
Since the probability space \(\Omega\) and any event \(A\subseteq \Omega\) are defined as sets, all operations applicable to sets, (e.g. union \(A\cup B\), intesection \(A\cap B\), complement \(\overline A\), etc.), are also applicable to events.
Therefore, it is notable that we can construct events from other events by combining them with set operations. The following table gives some answers and examples to the question, how these new events can be interpreted.

Interpretation of \(A \cap B\): The event that both events \(A\) and \(B\) occur at once, e.g.:
\(A=\) "It is raining.", \(B=\) "Today is my birthday." \(A \cap B=\) "It is raining AND today is my birthday."

Interpretation of \(A \cap B=\emptyset\): The impossible event, i.e. that the mutually exclusive events \(A\) and \(B\) occur at once, e.g.:
\(A=\) "It is raining.", \(B=\) "The street is dry." \(A \cap B=\) "It is raining AND the street is dry."

Interpretation of \(A\setminus B\): The event, when exactly \(A\) occurs and \(B\) does not occur, e.g.:
\(A=\) "It is raining.", \(B=\) "The street is dry." \(A \setminus B=\) "It is raining AND the street is NOT dry."

Interpretation of \(A \cup B\): The event that \(A\) occurs or \(B\) occurs, or both of them at once occur, e.g.:
\(A=\) "It is raining.", \(B=\) "The street is dry." \(A \setminus B=\) "It is raining OR the street is dry OR both)."
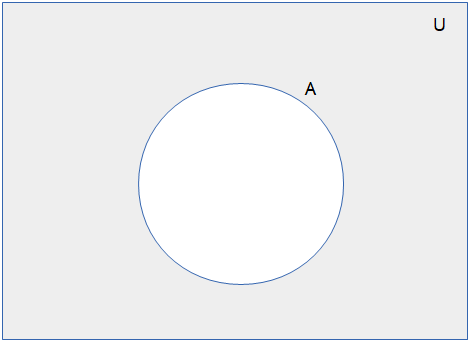
Interpretation of \(\overline A\): The event that \(A\) does not occur, e.g.:
\(A=\) "It is raining.", \(\overline A=\) "It is NOT raining."
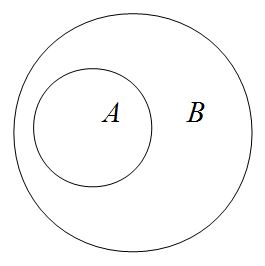
Interpretation of \(A\subseteq B\): If the event \(A\) occurs then certainly also \(B\) occurs, e.g.:
\(A=\) "It is raining.", \(B=\) "The street is wet." \(A \subseteq B=\) "The street is wet if it is raining."