Definition: Composition of Binary Relations

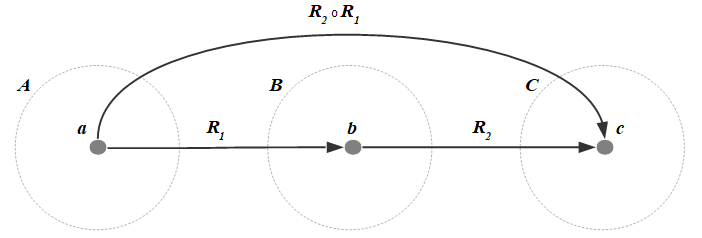
Let $A,B,C$ be sets and let let $R_1\subseteq A\times B$ and $R_2\subseteq B\times C$ be binary relations. If there are $a\in A,$ $b\in B,$ and $c\in C$ such that $aR_1b$ and $bR_2c,$ then there exists a binary relation $(R_2\circ R_1)\subseteq A\times C$ called the composition of the relations $R_1$ and $R_2$, and defined by this property $$(R_2\circ R_1):=\{(a,c)\in A\times C:aR_1b\;\wedge\;bR_2c,\;a\in A,\; b\in B,\; c\in C\}.$$

compositionrel