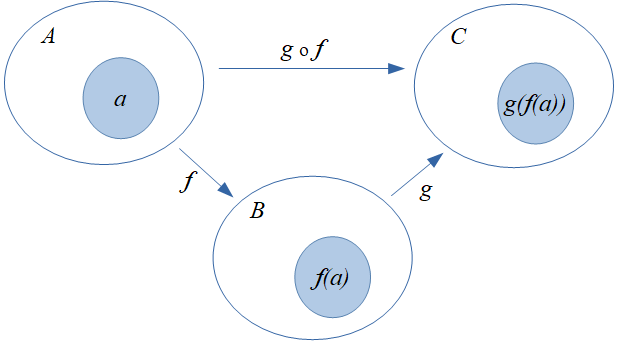
Let $A,B,C$ be sets. The following lemma shows that the composition of relations preserves the properties of a function.

Lemma: Composition of Functions

Let $f:A\mapsto B$ and $g:B\mapsto C$ be functions. The composition $g\circ f\subseteq A\times C$ of the corresponding relations $f\subseteq A\times B$ and $g\subseteq B\times C$ is also a function defined by

$$(g\circ f):A\to C,\;(g\circ f)(a):=g(f(a))$$

and called the composition of functions.

Examples

composition

If, for instance, $A=\mathbb R\to \mathbb R, f(x)=x^2$ and $g:\mathbb R\to \mathbb R, g(x)=x+2$, then $$(g\circ f)(x)=g(f(x))=g(x^2)=x^2+2,$$ and $$(f\circ g)(x)=f(g(x))=f(x+2)=x^2+2{x}+4.$$

Proofs: 1