The initial example, as well as the other examples show that the Mostowski function creates very different results on an ordered set $(X,\preceq),$ depending on the underlying well-founded relation $"\preceq".$ We want to make some observations, which will motivate a theorem of [Mostowski][mo].
[mo][https://mathshistory.st-andrews.ac.uk/Biographies/Mostowski/]# Motivation: Observation 1: The Mostowski Function Produces Transitive Sets
(related to Definition: Mostowski Function and Collapse)
Please note that in all four examples, the resulting Mostowski collapse $\pi([X])$ is a transitive set, i.e. if $x\in y$ and $y\in\pi([X])$, then $x\in \pi([X]).$
The Mostowski collapse was here the von Neumann set
$$\pi[\mathbb N]=\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\},\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\}\},\ldots \}.\quad ( * )$$
To see that this set is indeed transitive, note that all elements of this set obey a special construction principle: Starting with the empty set $\emptyset,$ the next set in the series after is \(\emptyset \cup \{\emptyset\}.\), and the specific construction principle \(X\cup \{X\}\) is repeated at every new element. We have already proven that \(X\cup \{X\}\) is transitive if \(X\) was. Since $\emptyset$ is transitive, by induction, the whole Mostowski collapse $( * )$ must be transitive. Moreover, even every element of the set $( * )$ is itself a transitive set.
The Mostowski collapse was here the set
$$\pi[\mathbb N]=\{\emptyset,\{\emptyset\},\{\{\emptyset\}\},\{\{\{\emptyset\}\}\},\ldots \}.\quad ( * * )$$
In contrast to the first example, in this set only the first two elements $\emptyset$ and $\{\emptyset\}$ are transitive, all other are not. But the Mostowski collapse $( * * )$ as a whole is transitive. In fact, we can combine any first \(n\) elements into new sets according to the following rule: \[T_0:=X_0,~T_n:=\bigcup_{0\le k\le n} X_k\] to produce transtive sets:
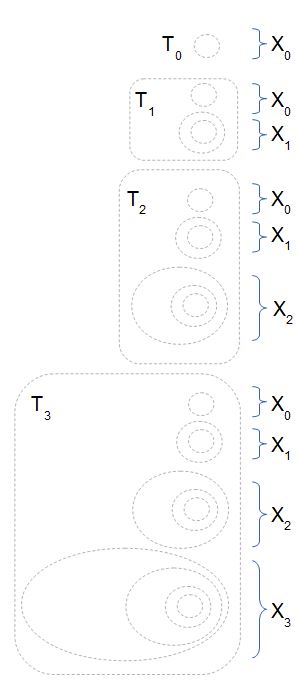
Now, for any \(T_n\) we have then: If \(X_k\in T_n\) for \(1\le k\le n\), then by definition \(X_k=\{X_{k-1}\}\). However, \(\{X_{k-1}\}\) is a subset of \(T_n\), so \(T_n\) is transitive.
The two Mostowski collapses in the examples were the sets
$$\pi[\mathcal P(\{a,b,c\})]=\{\emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\}, \{\emptyset, \{\emptyset\},\{\emptyset, \{\emptyset\}\}\}\}$$
and
$$\pi[X_k]=\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\}\}\quad\forall k.$$
These sets are transitive since they are the first elements of the von Neumann set in Example 1.
Theorems: 1