(related to Definition: Mostowski Function and Collapse)
The recursive nature of the Mostowski function makes it hard to imagine its effect of a given relation $R$. Moreover, it is at first sight not clear why the relation $R$ has to be well-founded. Let us start with answering the second question and try to create recursively the Mostowski function of a relation $R,$ which is not well-founded (in which we will fail!). As an example, let us take the partial order "$\le$" defined on the set of natural numbers $(\mathbb N,\le).$ Note, that there is no such subset $S\subset\mathbb N$ which has a minimal element. Even the subset $\{0\}\subset\mathbb N$ contains no minimal element, since $0\le 0,$ and, as you recall, a minimal element must be one that $\not\exists x\in \mathbb \{0\}\; x\le 0.$
Now, let us calculate the Mostowski function $\pi(0).$ By definition, $\pi(0)=\{\pi(m)\mid m\in\mathbb N\wedge m\le 0\}=\{\pi(0)\}.$ But hold on. By the axiom of foundation, every set $X$ is disjoint to its singleton $\{X\},$ i.e. we have to postulate $\pi(0)\cap \{\pi(0)\}=\emptyset.$ The above calculation $\pi(0)=\{\pi(0)\}$ contradicts the postulate, therefore we cannot create the Mostowski function of the not well-founded relation $"\le".$
The circumstances would be very different, if we changed the partial order "$\le" by the strict order $"<".$ Then $0$ would be minimal in the subset $\{0\}$ since there is no more such element $m\in \{0\}$ with $m < 0.$ Now, the Mostowski function $\pi(0)$ can be calculated. We use the first of the examples of well-founded relations:
By definition, $\pi(0)=\{\pi(m)\mid m\in\mathbb N\wedge m < 0\}=\emptyset.$ Let us calculate recursively some values for a couple of the first natural numbers:
$$\begin{array}{rcl} \pi(0)&=&\emptyset\\ \pi(1)&=&\{\pi(0)\}=\{\emptyset\}\\ \pi(2)&=&\{\pi(0),\pi(1)\}=\{\emptyset,\{\emptyset\}\}\\ \pi(3)&=&\{\pi(0),\pi(1),\pi(2)\}=\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\}\}\\ \pi(4)&=&\{\pi(0),\pi(1),\pi(2),\pi(3)\}=\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\},\{\emptyset,\{\emptyset\},\{\emptyset,\{\emptyset\}\}\}\}\\ &\vdots& \end{array}$$
Historically, this series of sets was used by von Neumann to define the natural numbers $\mathbb N$ and can be visualized as follows:
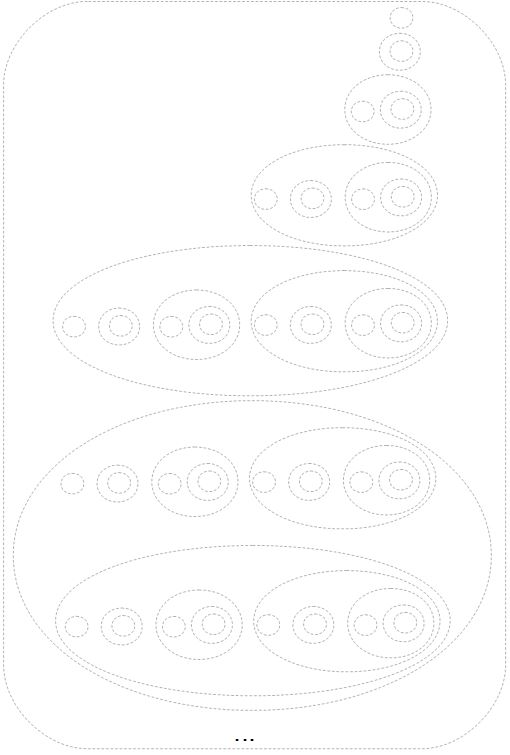
Loosely speaking, as "$n$ tends to infinity", for the strictly ordered set $(\mathbb N, <)$ the Mostowski function $\pi$ "tends" to a set we have already learned about as the minimal inductive set $\omega$. But what is the Mostowski collapse $(N, <)$ then? By definition, the Mostowski collapse of $(N, <)$ is the image of $\pi[\mathbb N],$ i.e. the set $W:=\{\pi(n)\mid n\in\mathbb N\}$. If $x\in W,$ then there is an $n\in\mathbb N$ with $x=\pi(n)$.
But note that then $x\cup \{x\}\in W.$ Therefore, $W$ is fulfilling the axiom of infinity and by definition, it is an inductive set. Since there are no other elements of $W$ than those produced by the Mostowski function $\pi$, $W$ corresponds exactly to the minimal inductive set $\omega$, i.e. we have $W=\omega$. In other words, $\omega$ is the Mostowski collapse of the function $\pi$. It is the "limit" of $\pi(n)$ as "$n$ tends to infinity."1
Of course, the notions "limit" and "to tend to infinity" are not defined here strict, and they are mathematical concepts known from analysis rather than from set theory. But we use them in this explanation anyway to help you to better understand the effect of the Mostowski function and collapse, using a wake idea of limit processes of "tending to". ↩