Before we discuss the properties of binary relations in general, we first introduce some ways to represent a given binary relation.# Explanation: Representations of Binary Relations
(related to Chapter: Binary Relations and Their Properties)
There are different possibilities to represent a binary relation $R\subseteq S\times T$. Sometimes, we can just enumerate the elements of \(R\). For instance, if \(S,T\) are bothe the set of natural numbers \(\mathbb N\) and \(R\) is the successor relation, then we can write \[R:=\{(1,2),(2,3),(3,4),\ldots \}\]
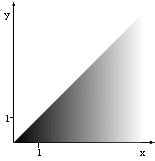
The figure below shows another representation of an infinite relation of all pairs of real numbers \(x,y\in\mathbb R\) satisfying the relation \(x\le y\).
If \(S, T\) have a finite number of elements, there are at least four possibilities to represent a relation. We demonstrate these possibilities for the divisibility relation \(R\) of all natural numbers between 1 and 10.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 :------------- |:------------- |:------------- |:------------- |:------------- |:------------- |:------------- |:------------- |:------------- |:------------- |:------------- 1| x| x| x| x| x| x| x| x| x| x 2| | x| | x| | x| | x| | x 3| | | x| | | x| | | x| 4| | | | x| | | | x| | 5| | | | | x| | | | | x 6| | | | | | x| | | | 7| | | | | | | x| | | 8| | | | | | | | x| | 9| | | | | | | | | x| 10| | | | | | | | | | x
\[M_R:=\left(\begin{array}{cccccccccc} 1&1&1&1&1&1&1&1&1&1\\ 0&1&0&1&0&1&0&1&0&1\\ 0&0&1&0&0&1&0&0&1&0\\ 0&0&0&1&0&0&0&1&0&0\\ 0&0&0&0&1&0&0&0&0&1\\ 0&0&0&0&0&1&0&0&0&0\\ 0&0&0&0&0&0&1&0&0&0\\ 0&0&0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&0&0&1\\ \end{array} \right)\]
Please note that the matrix of the inverse relation $R^{-1}$ corresponds to the transposed matrix of $M_R$. i.e.
\[M_{R^{-1}}=(M_R)^{T}=\left(\begin{array}{cccccccccc} 1&0&0&0&0&0&0&0&0&0\\ 1&1&0&0&0&0&0&0&0&0\\ 1&0&1&0&0&0&0&0&0&0\\ 1&1&0&1&0&0&0&0&0&0\\ 1&0&0&0&1&0&0&0&0&1\\ 1&1&1&0&0&1&0&0&0&0\\ 1&0&0&0&0&0&1&0&0&0\\ 1&1&0&1&0&0&0&1&0&0\\ 1&0&1&0&0&0&0&0&1&0\\ 1&1&0&0&0&0&0&0&0&1\\ \end{array} \right)\] In our case, this matrix represents the relation of numbers $(n,m)$ where $n$ is the multiple of $m.$
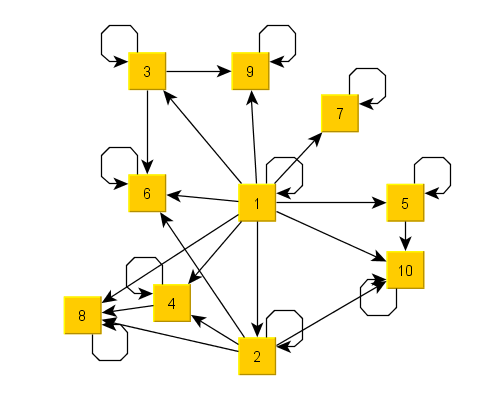
The digraph of the inverse relation is the same digraph with all arrows reversed.
is devisor of ... 1| \(\{1,2,3,4,5,6,7,8,9,10\}\) 2| \(\{2,4,6,8,10\}\) 3| \(\{3,6,9\}\) 4| \(\{4,8\}\) 5| \(\{5,10\}\) 6| \(\{6\}\) 7| \(\{7\}\) 8| \(\{8\}\) 9| \(\{9\}\) 10| \(\{10\}\)
Explanations: 1