(related to Definition: Pointwise and Uniform Convergence)
Let \((f_n)_{n\in\mathbb N}\) be a sequence of functions \(f_n:[ 0 , 1 ] \to \mathbb R\), defined for \(n\ge 2\) with
\[f_n(x):=\max\left(n-n^2\left|x-\frac 1n\right|,0\right).\]
The following figure shows the graph of one such function \(f_n\):
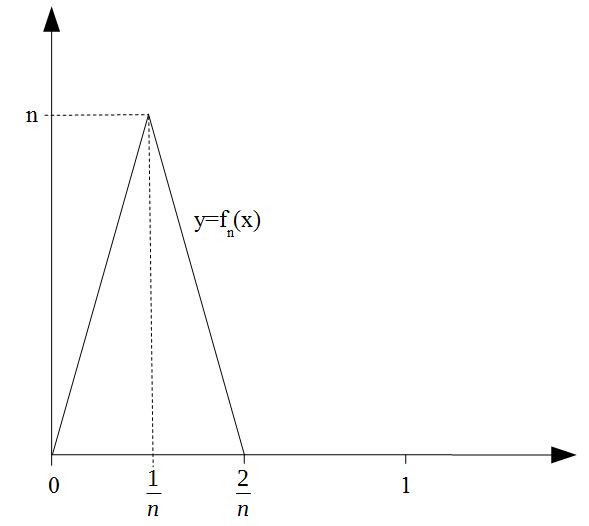
This sequence is pointwise convergent but it is not uniformly convergent.
We have to show that each \(x\in [0,1]\) and each \(\epsilon > 0\) there exists an \(N(x,\epsilon)\in\mathbb N\), such that \[|f_n(x) - f(x)| < \epsilon \text{ for all } n\ge N(x,\epsilon).\]
For \(x=0\), this is true since \(f_n(x)=0\) for all \(n\). Let \(x \in (0,1]\) and let \(\epsilon > 0\) be arbitrarily small. Since there is an \(N(x,\epsilon)\ge 2\) such that
\[\frac 2n\le x\quad\text{for all } n\ge N(x,\epsilon),\] we have \(f_n(x)=0\) for all \(n\ge N(x,\epsilon)\).
We have to show that there exists an \(\epsilon > 0\) and \(N(\epsilon)\in\mathbb N\), such that \[|f_n(x)-f(x)| \ge \epsilon \text{ for all } x\in [0,1]\text{ and all } n\ge N(\epsilon).\]
This is true for \(\epsilon = 1\) and \(N(\epsilon)=2\), because for every \(n\ge 2\) and for all \(x\in [0,1]\) we have \[|f_n(x)-0| > 1 .\]