Let \(\mathcal R=(\mathbb R,V_{\mathbb R},v)\) be an \(n\)-dimensional affine space with \(V_{\mathbb R}\) as the associated vector space over the field of real numbers \(\mathbb R\). Let \(P_0,P_1,P_2\ldots,P_s\) be \(s,\, (s\le n)\) affinely independent points. An \(s\)-dimensional simplex is the affine space defined by the barycentric coordinates. \[\sigma^s:=\{\lambda_0P_0+\cdots+\lambda_sP_s\,:\,\lambda_i\in \mathbb R, \, \lambda_i\ge 0,\,i=0,\ldots,s\,\wedge\, \lambda_0+\cdots+\lambda_s=1\}.\]
Please note that the definition of the \(s\)-dimensional simplex is almost the same as the definition of the whole affine span of the \(s\)-dimensional hyperplane
\[\{\lambda_0P_0+\cdots+\lambda_sP_s\,:\,\lambda_i\in \mathbb R, \,i=0,\ldots,s\,\wedge\, \lambda_0+\cdots+\lambda_s=1\},\]
except the additional condition that all \(\lambda_i\in \mathbb R\) must greater or equal \(0\).
If we choose \(m+1,\,m\le s\) points from the \(s+1\) points \(P_0,P_1,P_2\ldots,P_s\), then they also are affinely independent and form themselves a new simplex \(\sigma^m\), which is an affine subspace of the simplex \(\sigma^s\), called its \(m\)-face. The \(0\)-faces of \(\sigma^s\) are also called its vertices, the \(1\)-faces are called edges and its \(2\)-faces are called facets.
The following figure demonstrates some simplices \(\sigma^0\), \(\sigma^1\), \(\sigma^2\), and \(\sigma^3\):
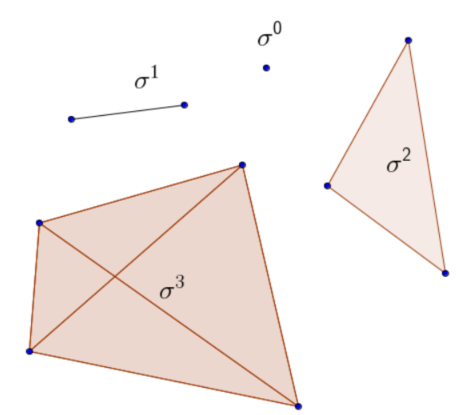
(c) bookofproofs own work