◀ ▲ ▶Branches / Algebra / Motivation: Calculations in a Group

Motivation: Calculations in a Group

(related to Chapter: Groups (Overview))

Before we dive deeper into the group theory, let us take a break from introducing new theoretical concepts. Instead, let us take a closer look at the algebraic structure in a group. If you are new to group theory but are familiar with arithmetics, you will recognize some parallels between the calculations which are possible in a group and calculations which are possible in a number system, for instance, the integers together with the addition $(\mathbb Z, + ).$ This is not a coincidence since number systems are groups.

We want to demonstrate this by the exampe of the number system of integers:

1. Adding two integers, e.g. $2 + 3$ will produce again an integer - here the result is $5.$ Therefore, $(\mathbb Z, + )$ is closed under the operation $"+".$
2. The addition of integers is associative.
3. Integer Zero $0$ is the neutral element of addition in $\mathbb Z$. For instance, $2+0=0+2=2.$
4. Moreover, every integer has an inverse. In our integer case, the inverse of $2$ is $-2$ and vice versa, since $2 + (-2)=(-2)+2=0.$ Therefore, negative and positive integers are inverse to each other and $0$ is inverse to itself.

These are exactly the properties required in a group. Therefore, $(\mathbb Z, + )$ is a group. It is even a commutative group, since the addition of integers is commutative. So far, so good. But if you are new to group theory, you will have to become aware of something else. Groups are algebraic structures, which can be arbitrary mathematical objects, not only numbers. In the general sense, groups might occur in sets which have nothing to do with numbers. The surprising fact is that also in these groups we can "calculate" with their elements as if they were numbers.

As an example, consider the set \(S,\ast\) of symmetries of an equilateral triangle, shown in the following figure:

• The element $a\in S$ can be interpreted as the identity symmetry (i.e. the neutral element of $S$) - we leave the triangle as it is.
• The element $b\in S$ is the rotation of the triangle by $120^\circ$ clockwise. You should convince yourself that $a=b\ast b\ast b=b^3,$ i.e. we have to rotate the triangle three times to get the original triangle again.
• Similarly, with $c\in S$ as the rotation of the triangle by $120^\circ$ counter-clockwise, we have $a=c\ast c\ast c=c^3.$
• The symmetries $d,e,f$ are not rotations but reflections. In the figure, the symmetry axis is drawn by a dotted line. We have $a=d^2=e^2=f^2.$
• On the other hand, all elements have also "inverse" elements, just like in the example of positive and negative integers above. For instance, the inverse reflections of \(d,e,f\) are inverse to themselves - i.e. composing one such reflection twice will result in the unchanged triangle (i.e. the symmetry \(a\)):

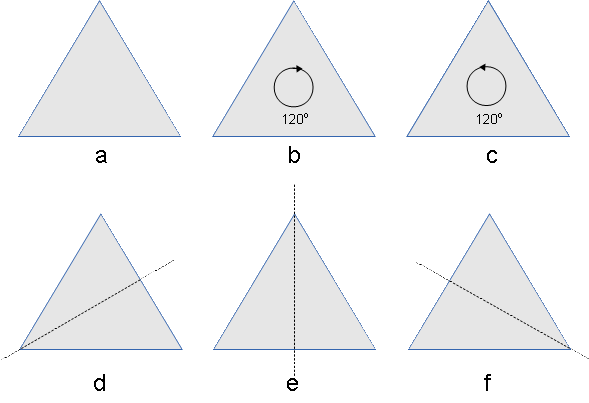
We can combine any of the six elements in an operation table of the group $(S,\ast)$ and you are invited to complete the table as an exercise:

$$\begin{array}{c|cccccc} \ast&a&b&c&d&e&f\\ \hline a&a&b&c&d&e&f\\ b&b&c&a&\text{(exercise)}&\text{(exercise)}&\text{(exercise)}\\ c&c&a&b&\text{(exercise)}&\text{(exercise)}&\text{(exercise)}\\ d&d&\text{(exercise)}&\text{(exercise)}&a&\text{(exercise)}&\text{(exercise)}\\ e&e&\text{(exercise)}&\text{(exercise)}&\text{(exercise)}&a&\text{(exercise)}\\ f&f&\text{(exercise)}&\text{(exercise)}&\text{(exercise)}&\text{(exercise)}&a\\ \end{array}$$

This example demonstrates that in groups we can "calculate" with elements exactly like we are used to in adding integers. In this sense, groups are a generalization of numbers.

Table of Contents

Explanations: 1

1. Proposition: Simple Calculations Rules in a Group
2. Definition: Exponentiation in a Group

Mentioned in:

Proofs: 1
Theorems: 2

Thank you to the contributors under CC BY-SA 4.0!

Github: