Let \(\mathcal A=(A,V_A,v)\) be an \(n\)-dimensional affine space with \(V_A\) as the associated vector space over the field \(\mathbb R\) of real numbers. A subset \(X\subseteq \mathcal A\) is called convex, if with any two points \(P,Q\in X\) it also contains the straight line segment \[\overline{PQ}:=\{\lambda P+(1-\lambda)Q\,|\,0\le\lambda\le 1\}\] between them. The following figure demonstrates a non-convex and a convex subset of the plane:
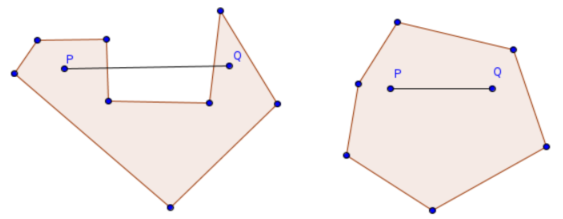
(c) bookofproofs own work
Corollaries: 1
Corollaries: 1
Definitions: 2 3 4 5 6
Proofs: 7