◀ ▲ ▶Branches / Analysis / Definition: Convex and Concave Functions

Definition: Convex and Concave Functions

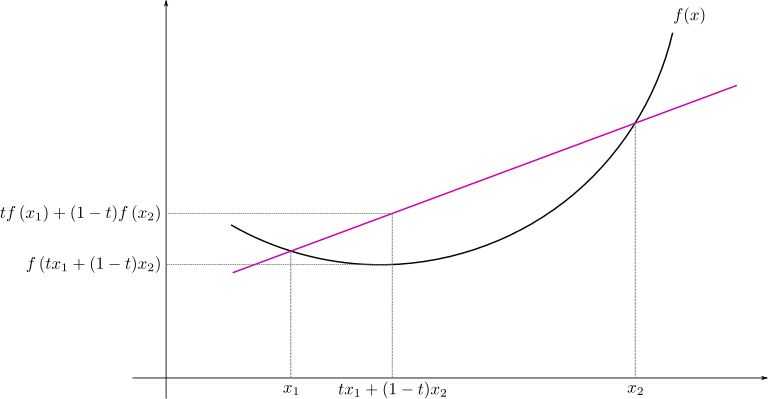
Let $D\subset\mathbb R$ be a real (finite or infinite) interval. A function $f:D\to\mathbb R$ is said to be convex on $D$, if $$f(t x_1 +(1-t)x_2)\le tf(x_1)+(1-t)f(x_2)$$ for all $x_1,x_2\in D$ and for all $0 < t < 1.$ The function $f$ is called concave if $-f$ is convex, i.e. if $$f(t x_1 +(1-t)x_2)\ge tf(x_1)+(1-t)f(x_2)$$ for all $0 < t < 1.$

From a graphical point of view, the condition means that (for $x_1 < x_2$) the graph of $f$ in the interval $[x_1,x_2]$ lies below the secant drawn through the points $(x_1,f(x_1))$, $(x_2,f(x_2))$ (see figure below):

From Wikimedia by Eli Osherovich

Table of Contents

1. Proposition: Convexity and Concaveness Test
2. Proposition: Convex Functions on Open Intervals are Continuous

Mentioned in:

Definitions: 1
Proofs: 2
Propositions: 3 4
Sections: 5

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Forster Otto: "Analysis 1, Differential- und Integralrechnung einer Veränderlichen", Vieweg Studium, 1983