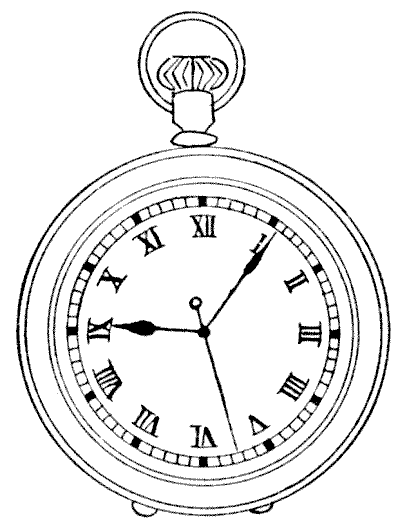
We have here a stop-watch with three hands. The second hand, which travels once around the face in a minute, is the one with the little ring at its end near the center. Our dial indicates the exact time when its owner stopped the watch. You will notice that the three hands are nearly equidistant. The hour and minute hands point to spots that are exactly a third of the circumference apart, but the second hand is a little too advanced. An exact equidistance for the three hands is not possible. Now, we want to know what the time will be when the three hands are next at exactly the same distances as shown from one another. Can you state the time?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.