The puzzle is to place a different number in each of the ten squares so that the sum of the squares of any two adjacent numbers shall be equal to the sum of the squares of the two numbers diametrically opposite to them. The four numbers placed, as examples, must stand as they are. The square of $16$ is $256,$ and the square of $2$ is $4.$ Add these together, and the result is $260.$ Also—the square of $14$ is $196,$ and the square of $8$ is $64.$ These together also make $260.$ Now, in precisely the same way, $B$ and $C$ should be equal to $G$ and $H$ (the sum will not necessarily be $260$), $A$ and $K$ to $F$ and $E,$ $H$ and $I$ to $C$ and $D,$ and so on, with any two adjoining squares in the circle.
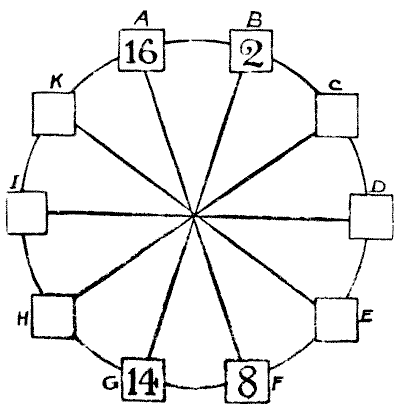
All you have to do is to fill in the remaining six numbers. Fractions are not allowed, and I shall show that no number need contain more than two figures.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.