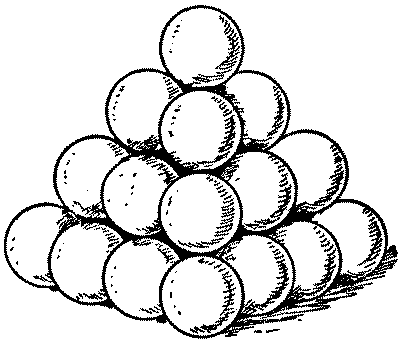
"All cannon-balls are to be piled in square pyramids," was the order issued to the regiment. This was done. Then came the further order, "All pyramids are to contain a square number of balls." Whereupon the trouble arose. "It can't be done," said the major. "Look at this pyramid, for example; there are sixteen balls at the base, then nine, then four, then one at the top, making thirty balls in all. But there must be six more balls, or five fewer, to make a square number." "It must be done," insisted the general. "All you have to do is to put the right number of balls in your pyramids." "I've got it!" said a lieutenant, the mathematical genius of the regiment. "Lay the balls out singly." "Bosh!" exclaimed the general. "You can't pile one ball into a pyramid!" Is it really possible to obey both orders?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.