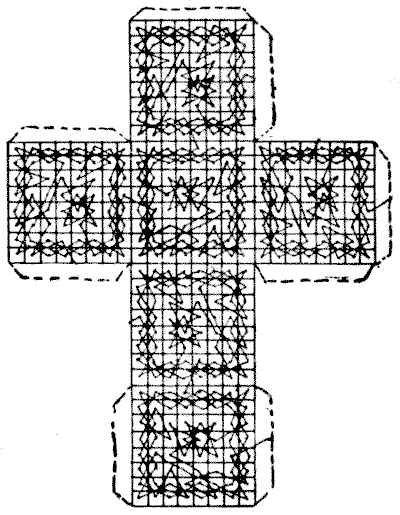
(related to Problem: The Cubic Knight's Tour)
If the reader should cut out the above diagram, fold it in the form of a cube, and stick it together by the strips left for that purpose at the edges, he would have an interesting little curiosity. Or he can make one on a larger scale for himself. It will be found that if we imagine the cube to have a complete chessboard on each of its sides, we may start with the knight on any one of the $384$ squares, and make a complete tour of the cube, always returning to the starting-point. The method of passing from one side of the cube to another is easily understood, but, of course, the difficulty consisted in finding the proper points of entry and exit on each board, the order in which the different boards should be taken, and in getting arrangements that would comply with the required conditions.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.