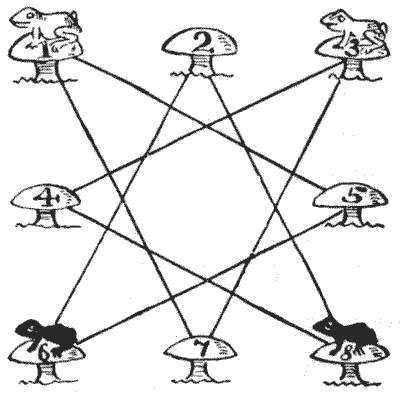
In the illustration, we have eight toadstools, with white frogs on $1$ and $3$ and black frogs on $6$ and $8.$ The puzzle is to move one frog at a time, in any order, along one of the straight lines from toadstool to toadstool, until they have exchanged places, the white frogs being left on $6$ and $8$ and the black ones on $1$ and $3.$ If you use four counters on a simple diagram, you will find this quite easy, but it is a little more puzzling to do it in only seven plays, any number of successive moves by one frog counting as one play. Of course, more than one frog cannot be on a toadstool at the same time.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.