A man has twenty-five dog kennels all communicating with each other by doorways, as shown in the illustration. He wishes to arrange his twenty dogs so that they shall form a knight's string from dog No. $1$ to dog No. $20,$ the bottom row of five kennels to be left empty, as at present. This is to be done by moving one dog at a time into a vacant kennel.
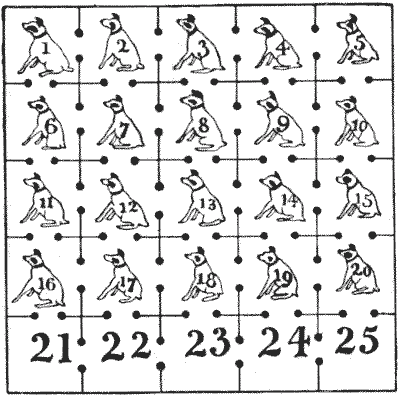
The dogs are well trained to obedience and may be trusted to remain in the kennels in which they are placed, except that if two are placed in the same kennel together they will fight it out to the death. How is the puzzle to be solved in the fewest possible moves without two dogs ever being together?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.