(related to Problem: The Kennel Puzzle)
The first point is to make a choice of the most promising knight's string and then consider the question of reaching the arrangement in the fewest moves. I am strongly of opinion that the best string is the one represented in the following diagram, in which it will be seen that each successive number is a knight's move from the preceding one and that five of the dogs $(1, 5, 10, 15,$ and $20)$ never leave their original kennels.
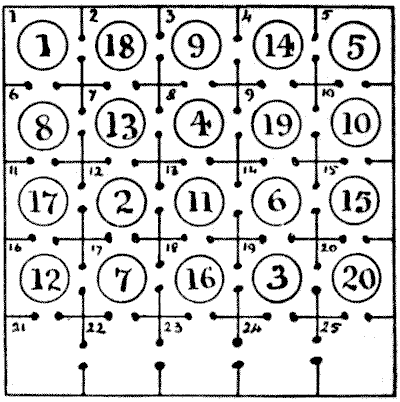
This position may be arrived at in as few as forty-six moves, as follows: $16—21,$ $16—22,$ $16—23,$ $17—16,$ $12—17,$ $12—22,$ $12—21,$ $7—12,$ $7—17,$ $7—22,$ $11—12,$ $11—17,$ $2—7,$ $2—12,$ $6—11,$ $8—7,$ $8—6,$ $13—8,$ $18—13,$ $11—18,$ $2—17,$ $18—12,$ $18—7,$ $18—2,$ $13—7,$ $3—8,$ $3—13,$ $4—3,$ $4—8,$ $9—4,$ $9—3,$ $14—9,$ $14—4,$ $19—14,$ $19—9,$ $3—14,$ $3—19,$ $6—12,$ $6—13,$ $6—14,$ $17—11,$ $12—16,$ $2—12,$ $7—17,$ $11—13,$ $16—18 = 46$ moves. I am, of course, not able to say positively that a solution cannot be discovered in fewer moves, but I believe it will be found a very hard task to reduce the number.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.