(related to Problem: The Bun Puzzle)
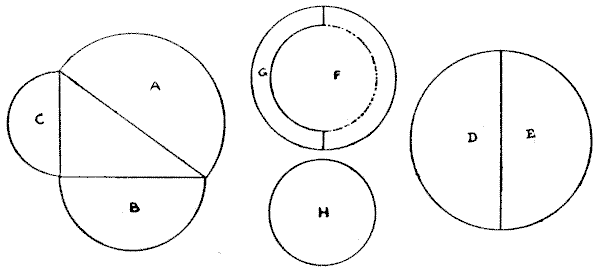
The secret of the bun puzzle lies in the fact that, with the relative dimensions of the circles as given, the three diameters will form a right-angled triangle, as shown by $A, B, C.$ It follows that the two smaller buns are exactly equal to the large bun. Therefore, if we give David and Edgar the two halves marked $D$ and $E,$ they will have their fair shares — one quarter of the confectionery each. Then if we place the small bun, $H,$ on the top of the remaining one and trace its circumference in the manner shown, Fred's piece, $F,$ will exactly equal Harry's small bun, $H,$ with the addition of the piece marked $G$ — half the rim of the other. Thus each boy gets an exactly equal share, and there are only five pieces necessary.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.